2192. All Ancestors of a Node in a Directed Acyclic Graph

Problem

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.

Return a list answer**, where *answer[i]* is the list of ancestors of the** ith **node, sorted in *ascending order***.

A node u is an ancestor of another node v if u can reach v via a set of edges.

  Example 1:

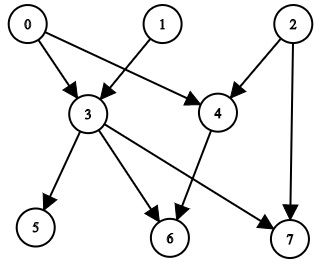
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

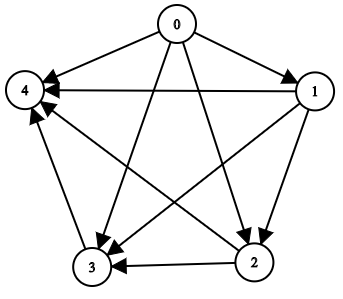
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.

  Constraints:

• 1 <= n <= 1000

• 0 <= edges.length <= min(2000, n * (n - 1) / 2)

• edges[i].length == 2

• 0 <= fromi, toi <= n - 1

• fromi != toi

• There are no duplicate edges.

• The graph is directed and acyclic.

Solution

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[][]}
 */
var getAncestors = function(n, edges) {
    const parentMap = Array(n).fill(0).map(() => []);
    const ancestorMap = Array(n);
    for (var i = 0; i < edges.length; i++) {
        parentMap[edges[i][1]].push(edges[i][0]);
    }
    for (var i = 0; i < n; i++) {
        find(i, parentMap, ancestorMap);
    }
    return ancestorMap.map(item => item.sort((a, b) => a - b));
};

var find = function(i, parentMap, ancestorMap) {
    if (!ancestorMap[i]) {
        var res = [];
        var arr = parentMap[i];
        for (var j = 0; j < arr.length; j++) {
            res.push(arr[j], ...find(arr[j], parentMap, ancestorMap));
        }
        ancestorMap[i] = Array.from(new Set(res));
    }
    return ancestorMap[i];
};

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).