894. All Possible Full Binary Trees

Problem

Given an integer n, return **a list of all possible *full binary trees* with** n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

  Example 1:

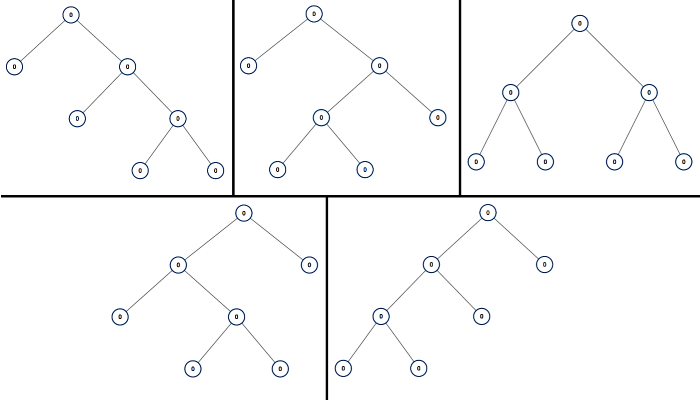
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Example 2:

Input: n = 3
Output: [[0,0,0]]

  Constraints:

• 1 <= n <= 20

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number} n
 * @return {TreeNode[]}
 */
var allPossibleFBT = function(n) {
    var dp = Array(n);
    dp[0] = [new TreeNode()];
    return solve(n, dp);
};

var solve = function(n, dp) {
    if (dp[n - 1]) return dp[n - 1];
    var res = [];
    for (var i = 1; i < n - 1; i += 2) {
        var left = solve(i, dp);
        var right = solve(n - 1 - i, dp);
        for (var j = 0; j < left.length; j++) {
            for (var m = 0; m < right.length; m++) {
                res.push(new TreeNode(0, left[j], right[m]));
            }
        }
    }
    dp[n - 1] = res;
    return res;
};

Explain:

Bottom-up with dynamic programming.

Complexity:

• Time complexity : O(2 ^ (n / 2)).
• Space complexity : O(n * 2 ^ (n / 2)).