Problem
There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.
Return the number of bulbs that are on after n rounds.
Example 1:
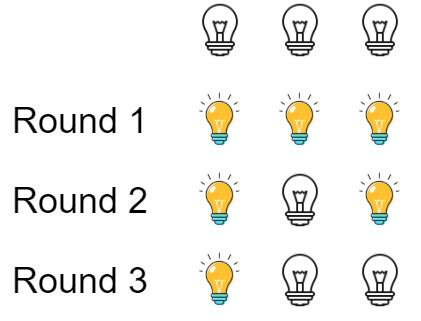
Input: n = 3
Output: 1
Explanation: At first, the three bulbs are [off, off, off].
After the first round, the three bulbs are [on, on, on].
After the second round, the three bulbs are [on, off, on].
After the third round, the three bulbs are [on, off, off].
So you should return 1 because there is only one bulb is on.
Example 2:
Input: n = 0
Output: 0
Example 3:
Input: n = 1
Output: 1
Constraints:
0 <= n <= 109
Solution
/**
* @param {number} n
* @return {number}
*/
var bulbSwitch = function(n) {
return Math.floor(Math.sqrt(n));
};
Explain:
For the kth bulb, it is switched exactly a number of times that is a divisor of k. If k has an even number of divisors, then the final state of the kth light bulb is dark; if k has an odd number of divisors, then the final state of the kth light bulb is bright.
For k, if it has divisor x, then there must be divisor k/x. Therefore, as long as at that time, divisors appear in "pairs". This means that only when k is a "perfect square number", it will have an odd number of divisors, otherwise it must have an even number of divisors.
Therefore, we only need to find out the number of perfect square numbers in 1 ~ n, and the answer is sqrt(n)
Complexity:
- Time complexity : O(1).
- Space complexity : O(1).