787. Cheapest Flights Within K Stops

Problem

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return **the cheapest price from src to dst with at most k stops. If there is no such route, return **-1.

  Example 1:

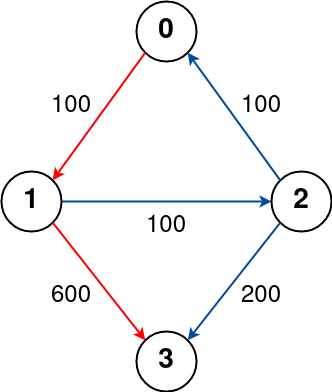
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2:

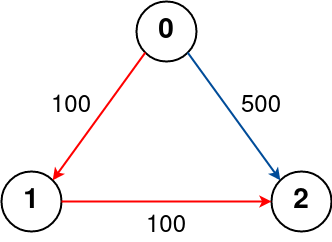
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3:

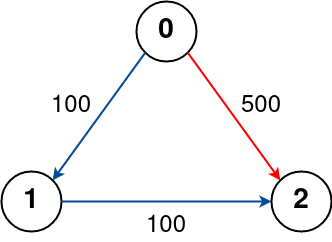
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

  Constraints:

• 1 <= n <= 100

• 0 <= flights.length <= (n * (n - 1) / 2)

• flights[i].length == 3

• 0 <= fromi, toi < n

• fromi != toi

• 1 <= pricei <= 104

• There will not be any multiple flights between two cities.

• 0 <= src, dst, k < n

• src != dst

Solution

/**
 * @param {number} n
 * @param {number[][]} flights
 * @param {number} src
 * @param {number} dst
 * @param {number} k
 * @return {number}
 */
var findCheapestPrice = function(n, flights, src, dst, k) {
    var map = Array(n).fill(0).map(() => []);
    for (var i = 0; i < flights.length; i++) {
        map[flights[i][0]].push([flights[i][1], flights[i][2]]);
    }
    var dp = Array(n).fill(0).map(() => ({}));
    var res = dfs(src, dst, k, map, dp);
    return res;
};

var dfs = function(src, dst, k, map, dp) {
    if (dp[src][k] !== undefined) return dp[src][k];
    if (src === dst) return 0;
    if (k === -1) return -1;
    var res = -1;
    for (var i = 0; i < map[src].length; i++) {
        var tmp = dfs(map[src][i][0], dst, k - 1, map, dp);
        if (tmp === -1) continue;
        if (res === -1 || res > tmp + map[src][i][1]) {
            res = tmp + map[src][i][1];
        }
    }
    dp[src][k] = res;
    return res;
};

Explain:

DFS + DP.

Complexity:

• Time complexity : O(n * k).
• Space complexity : O(n * k).