Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Problem

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

Example 1:

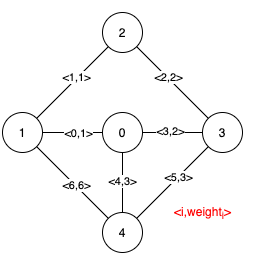
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

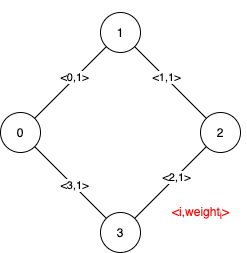
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

Constraints:

2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= ai < bi < n
1 <= weighti <= 1000
All pairs (ai, bi) are distinct.

Solution

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[][]}
 */
var findCriticalAndPseudoCriticalEdges = function(n, edges) {
    var [min] = findMinSpanningTreeWeight(n, edges);
    var res = [[], []];
    for (var i = 0; i < edges.length; i++) {
        var [num, parents] = findMinSpanningTreeWeight(n, edges, undefined, edges[i]);
        var root = find(parents, 0);
        var isCritical = num > min || !Array(n).fill(0).every((_, k) => find(parents, k) === root);
        if (isCritical) {
            res[0].push(i);
        } else {
            var [num2] = findMinSpanningTreeWeight(n, edges, edges[i], undefined);
            if (num2 === min) res[1].push(i);
        }
    }
    return res;
};

var findMinSpanningTreeWeight = function(n, edges, mustHaveItem, mustNotHaveItem) {
    edges = [...edges];
    edges.sort((a, b) => a[2] - b[2]);

    if (mustHaveItem !== undefined) {
        edges = edges.filter((item) => item !== mustHaveItem);
        edges.unshift(mustHaveItem);
    }

    var res = 0;
    var parents = Array(n).fill(0).map((_, i) => i);
    var count = Array(n).fill(0);
    for (var i = 0; i < edges.length; i++) {
        if (edges[i] === mustNotHaveItem) continue;
        var [m, k, distance] = edges[i];
        var j = find(parents, m);
        var p = find(parents, k);
        if (j === p) continue;
        if (count[j] <= count[p]) {
            union(parents, j, p);
            count[p]++;
        } else {
            union(parents, p, j);
            count[j]++;
        }
        res += distance;
    }

    return [res, parents];
};

var find = function(parents, i) {
    if (parents[i] === i) return i
    parents[i] = find(parents, parents[i]);
    return parents[i];
};

var union = function(parents, i, j) {
    parents[i] = j;
};

Explain:

nope.

Complexity:

Time complexity : O(m * n ^ 2).
Space complexity : O(n ^ 2).