785. Is Graph Bipartite?

Problem

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).

• There are no parallel edges (graph[u] does not contain duplicate values).

• If v is in graph[u], then u is in graph[v] (the graph is undirected).

• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true** if and only if it is bipartite**.

  Example 1:

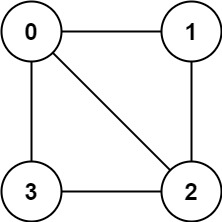
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

  Constraints:

• graph.length == n

• 1 <= n <= 100

• 0 <= graph[u].length < n

• 0 <= graph[u][i] <= n - 1

• graph[u] does not contain u.

• All the values of graph[u] are unique.

• If graph[u] contains v, then graph[v] contains u.

Solution

/**
 * @param {number[][]} graph
 * @return {boolean}
 */
var isBipartite = function(graph) {
    var map = {};
    for (var i = 0; i < graph.length; i++) {
        if (!dfs(graph, map, i)) return false;
    }
    return true;
};

var dfs = function(graph, map, i, group) {
    if (map[i]) return !group || group === map[i];
    map[i] = group || 1;
    for (var j = 0; j < graph[i].length; j++) {
        if (!dfs(graph, map, graph[i][j], map[i] === 1 ? 2 : 1)) return false;
    }
    return true;
};

Explain:

DFS with memorize.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).