1727. Largest Submatrix With Rearrangements

Problem

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return **the area of the largest submatrix within *matrix* where every element of the submatrix is 1 after reordering the columns optimally.**

  Example 1:

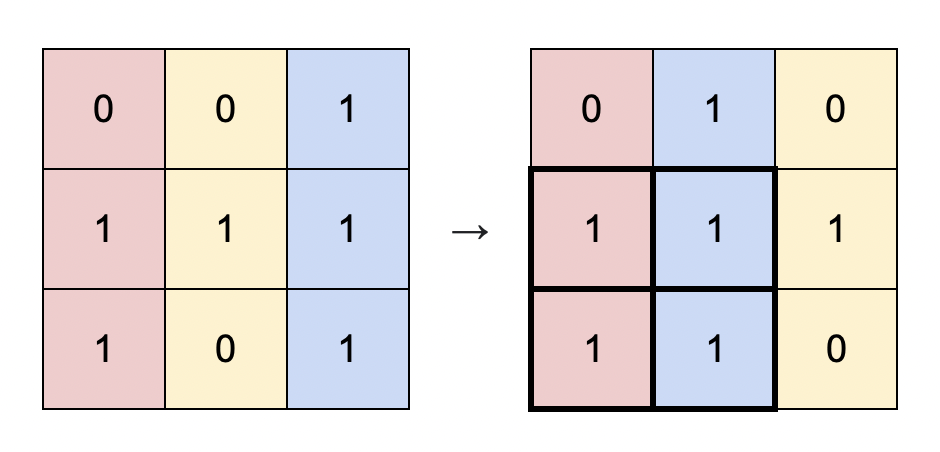
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

  Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m * n <= 105

• matrix[i][j] is either 0 or 1.

Solution 1

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var largestSubmatrix = function(matrix) {
    var max = 0;
    for (var i = 0; i < matrix.length; i++) {
        for (var j = 0; j < matrix[i].length; j++) {
            if (matrix[i][j] !== 0 && i > 0) {
                matrix[i][j] = matrix[i - 1][j] + 1;
            }
        }
        var arr = [...matrix[i]].sort((a, b) => b - a);
        for (var j = 0; j < arr.length; j++) {
            if (arr[j] === 0) break;
            max = Math.max(max, arr[j] * (j + 1));
        }
    }
    return max;
};

Explain:

nope.

Complexity:

• Time complexity : O(n * m * log(m)).
• Space complexity : O(1).

Solution 2

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var largestSubmatrix = function(matrix) {
    var max = 0;
    var lastHeights = [];
    for (var i = 0; i < matrix.length; i++) {
        var seen = {};
        for (var j = 0; j < matrix[i].length; j++) {
            if (matrix[i][j] === 1) {
                i > 0 && (matrix[i][j] = matrix[i - 1][j] + 1);
                seen[j] = true;
            }
        }
        var heights = [];
        // old ones
        var used = {};
        for (var k = 0; k < lastHeights.length; k++) {
            var item = lastHeights[k];
            if (seen[item[1]]) {
                heights.push([item[0] + 1, item[1]]);
                used[item[1]] = true;
            }
        }
        // new ones
        var keys = Object.keys(seen);
        for (var n = 0; n < keys.length; n++) {
            if (!used[keys[n]]) {
                heights.push([1, Number(keys[n])]);
            }
        }
        for (var m = 0; m < heights.length; m++) {
            max = Math.max(max, heights[m][0] * (m + 1));
        }
        lastHeights = heights;
    }
    return max;
};

Explain:

nope.

Complexity:

• Time complexity : O(n * m).
• Space complexity : O(m).