1751. Maximum Number of Events That Can Be Attended II

Problem

You are given an array of events where events[i] = [startDayi, endDayi, valuei]. The ith event starts at startDayi and ends at endDayi, and if you attend this event, you will receive a value of valuei. You are also given an integer k which represents the maximum number of events you can attend.

You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.

Return **the *maximum sum* of values that you can receive by attending events.**

  Example 1:

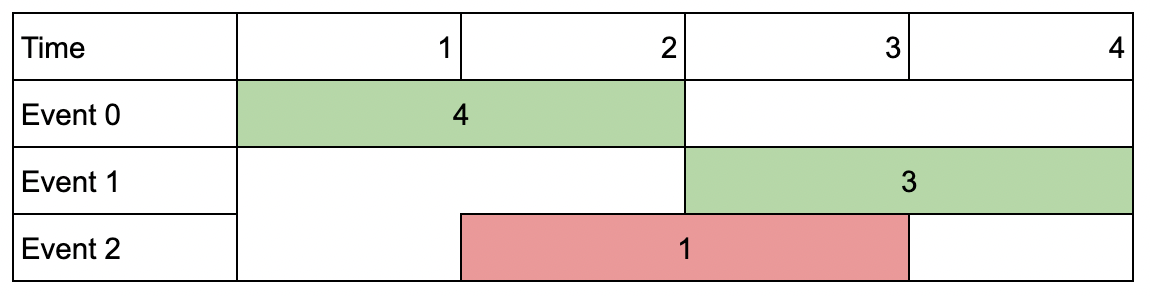
Input: events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output: 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.

Example 2:

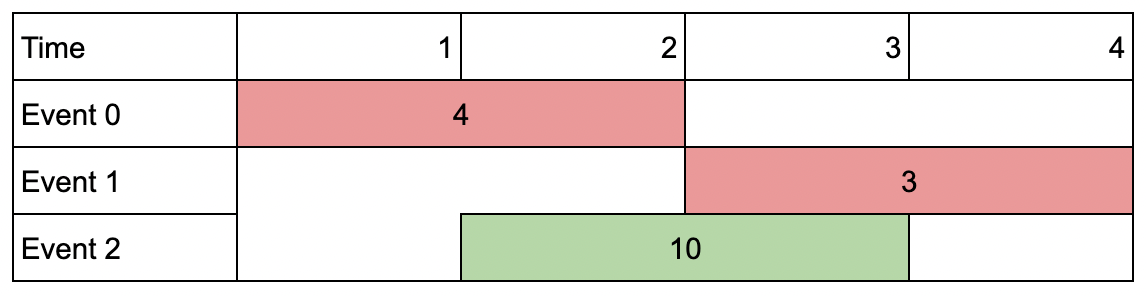
Input: events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output: 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do not have to attend k events.

Example 3:

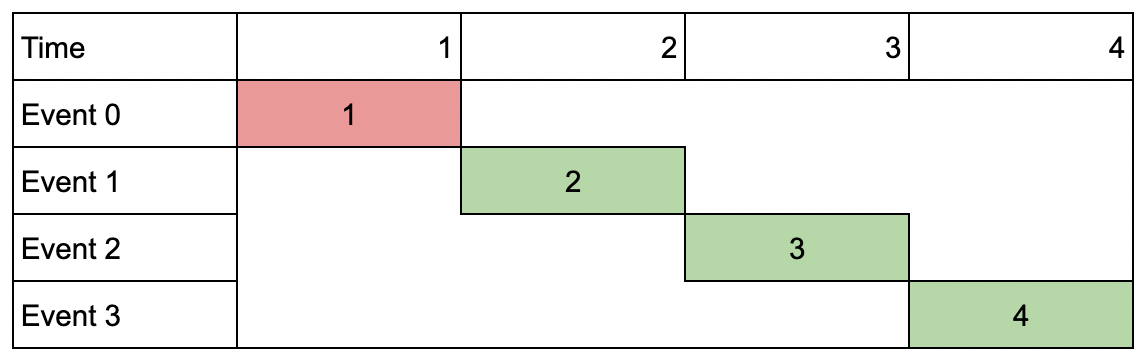
Input: events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output: 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.

  Constraints:

• 1 <= k <= events.length

• 1 <= k * events.length <= 106

• 1 <= startDayi <= endDayi <= 109

• 1 <= valuei <= 106

Solution

/**
 * @param {number[][]} events
 * @param {number} k
 * @return {number}
 */
var maxValue = function(events, k) {
    var dp = Array(events.length).fill(0).map(() => Array(k));
    events.sort((a, b) => a[0] - b[0]);
    return dfs(events, k, dp, 0, 0);
};

var dfs = function(events, k, dp, index, count) {
    if (count >= k || index >= events.length || index < 0) return 0;
    if (dp[index][count] !== undefined) return dp[index][count];
    dp[index][count] = Math.max(
        dfs(events, k, dp, index + 1, count),
        events[index][2] + dfs(events, k, dp, find(events, index), count + 1)
    );
    return dp[index][count];
};

var find = function(events, index) {
    for (var i = index + 1; i < events.length; i++) {
        if (events[i][0] > events[index][1]) return i;
    }
    return -1;
};

Explain:

DFS with DP.

Complexity:

• Time complexity : O(k * n * n).
• Space complexity : O(k * n).

Solution 2

/**
 * @param {number[][]} events
 * @param {number} k
 * @return {number}
 */
var maxValue = function(events, k) {
    var dp = Array(events.length).fill(0).map(() => Array(k));
    events.sort((a, b) => a[0] - b[0]);
    return dfs(events, k, dp, 0, 0);
};

var dfs = function(events, k, dp, index, count) {
    if (count >= k || index >= events.length || index < 0) return 0;
    if (dp[index][count] !== undefined) return dp[index][count];
    dp[index][count] = Math.max(
        dfs(events, k, dp, index + 1, count),
        events[index][2] + dfs(events, k, dp, find(events, index), count + 1)
    );
    return dp[index][count];
};

var find = function(events, index) {
    var left = index + 1;
    var right = events.length - 1;
    while (left <= right) {
        var mid = left + Math.floor((right - left) / 2);
        if (events[mid][0] > events[index][1]) {
            if (right === left) return mid;
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return -1;
};

Explain:

DFS with DP and Binary Search.

Complexity:

• Time complexity : O(k * n * log(n)).
• Space complexity : O(k * n).