2684. Maximum Number of Moves in a Grid

Problem

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return **the *maximum* number of moves that you can perform.**

  Example 1:

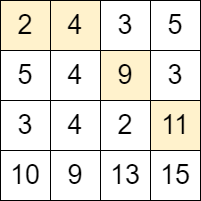
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

  Constraints:

• m == grid.length

• n == grid[i].length

• 2 <= m, n <= 1000

• 4 <= m * n <= 105

• 1 <= grid[i][j] <= 106

Solution

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxMoves = function(grid) {
    var dp = Array(grid.length).fill(0).map(() => Array(grid[0].length));
    var max = 0;
    for (var i = 0; i < grid.length; i++) {
        max = Math.max(max, helper(grid, i, 0, dp));
    }
    return max;
};

var helper = function(grid, i, j, dp) {
    if (dp[i][j] !== undefined) return dp[i][j];
    var max = 0;
    if (j < grid[0].length - 1) {
        if (i > 0 && grid[i - 1][j + 1] > grid[i][j]) {
            max = Math.max(max, 1 + helper(grid, i - 1, j + 1, dp));
        }
        if (grid[i][j + 1] > grid[i][j]) {
            max = Math.max(max, 1 + helper(grid, i, j + 1, dp));
        }
        if (i < grid.length - 1 && grid[i + 1][j + 1] > grid[i][j]) {
            max = Math.max(max, 1 + helper(grid, i + 1, j + 1, dp));
        }
    }
    dp[i][j] = max;
    return max;
};

Explain:

nope.

Complexity:

• Time complexity : O(m * n).
• Space complexity : O(m * n).