Problem
Given an n x n integer matrix grid, return **the minimum sum of a *falling path with non-zero shifts***.
A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.
Example 1:
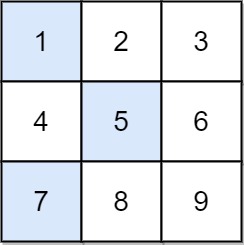
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: 13
Explanation:
The possible falling paths are:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
The falling path with the smallest sum is [1,5,7], so the answer is 13.
Example 2:
Input: grid = [[7]]
Output: 7
Constraints:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
Solution
/**
* @param {number[][]} grid
* @return {number}
*/
var minFallingPathSum = function(grid) {
for (var i = 1; i < grid.length; i++) {
var [minIndex, secondMinIndex] = findMinIndexs(grid[i - 1]);
for (var j = 0; j < grid[i].length; j++) {
grid[i][j] += grid[i - 1][minIndex === j ? secondMinIndex : minIndex];
}
}
return Math.min(...grid[grid.length - 1]);
};
var findMinIndexs = function(arr) {
var minIndex = arr[0] > arr[1] ? 1 : 0;
var secondMinIndex = arr[0] > arr[1] ? 0 : 1;
for (var i = 2; i < arr.length; i++) {
if (arr[i] < arr[minIndex]) {
secondMinIndex = minIndex;
minIndex = i;
} else if (arr[i] < arr[secondMinIndex]) {
secondMinIndex = i;
}
}
return [minIndex, secondMinIndex];
};
Explain:
nope.
Complexity:
- Time complexity : O(n * m).
- Space complexity : O(1).