Problem
Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.
Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
Example 1:
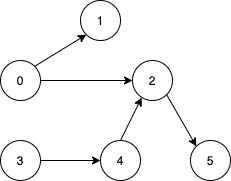
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].
Example 2:
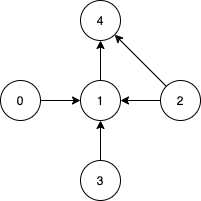
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
Constraints:
2 <= n <= 10^51 <= edges.length <= min(10^5, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi < nAll pairs
(fromi, toi)are distinct.
Solution
/**
* @param {number} n
* @param {number[][]} edges
* @return {number[]}
*/
var findSmallestSetOfVertices = function(n, edges) {
var map = Array(n).fill(0);
for (var i = 0; i < edges.length; i++) {
map[edges[i][1]]++;
}
var res = [];
for (var j = 0; j < n; j++) {
if (map[j] === 0) {
res.push(j);
}
}
return res;
};
Explain:
Because it's guaranteed that a unique solution exists, so we can simply collect nodes with no incoming edge.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).