1824. Minimum Sideway Jumps

Problem

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the **second *lane* **and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

• For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

• For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return** the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.**

Note: There will be no obstacles on points 0 and n.

  Example 1:

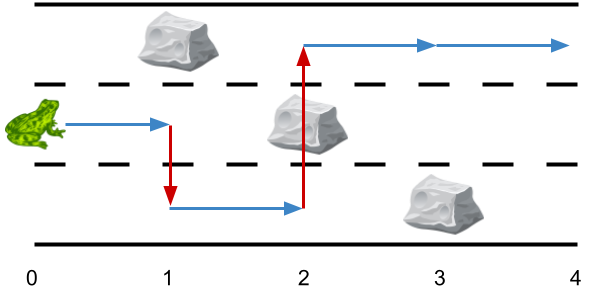
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2:

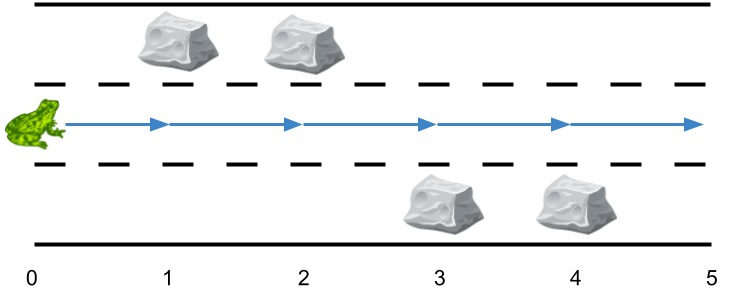
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3:

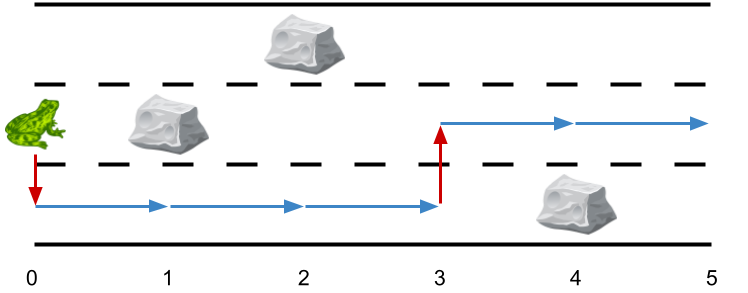
Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

  Constraints:

• obstacles.length == n + 1

• 1 <= n <= 5 * 105

• 0 <= obstacles[i] <= 3

• obstacles[0] == obstacles[n] == 0

Solution

/**
 * @param {number[]} obstacles
 * @return {number}
 */
var minSideJumps = function(obstacles) {
    return helper(obstacles, 0, 2);
};

var helper = function(obstacles, i, lane) {
    if (i === obstacles.length) return 0;
    if (obstacles[i + 1] !== lane) return helper(obstacles, i + 1, lane);
    var nextIndex = -1;
    for (var j = i; j < obstacles.length; j++) {
        if (obstacles[j] !== lane && obstacles[j] !== 0) {
            nextIndex = j;
            break;
        }
    }
    if (nextIndex === -1) return 1;
    return 1 + helper(obstacles, nextIndex, 6 - lane - obstacles[nextIndex]);
};

Explain:

Greedy.

Complexity:

• Time complexity : O(n).
• Space complexity : O(1).