1361. Validate Binary Tree Nodes

Problem

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

  Example 1:

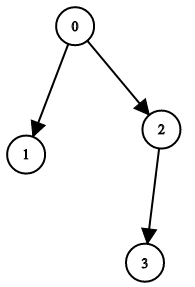
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

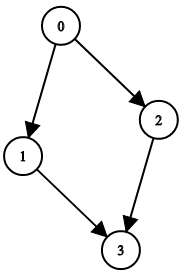
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

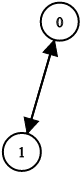
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

  Constraints:

• n == leftChild.length == rightChild.length

• 1 <= n <= 104

• -1 <= leftChild[i], rightChild[i] <= n - 1

Solution

/**
 * @param {number} n
 * @param {number[]} leftChild
 * @param {number[]} rightChild
 * @return {boolean}
 */
var validateBinaryTreeNodes = function(n, leftChild, rightChild) {
    var indegree = Array(n).fill(0);
    for (var i = 0; i < n; i++) {
        leftChild[i] !== -1 && indegree[leftChild[i]]++;
        rightChild[i] !== -1 && indegree[rightChild[i]]++;
    }
    var root = indegree.findIndex(num => num === 0);
    var visited = Array(n).fill(false);
    var visit = function(node) {
        if (visited[node]) return false;
        visited[node] = true;
        return (leftChild[node] === -1 || visit(leftChild[node]))
            && (rightChild[node] === -1 || visit(rightChild[node]));
    };
    return visit(root) && visited.every(n => n);
};

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).