Problem
Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.
If the tree has more than one mode, return them in any order.
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than or equal to the node's key.
The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
Both the left and right subtrees must also be binary search trees.
Example 1:
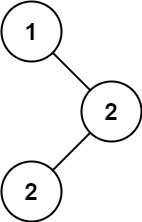
Input: root = [1,null,2,2]
Output: [2]
Example 2:
Input: root = [0]
Output: [0]
Constraints:
The number of nodes in the tree is in the range
[1, 104].-105 <= Node.val <= 105
Follow up: Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
Solution
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var findMode = function(root) {
var max = 0;
var res = [];
var num = 0.1;
var count = 0;
var update = () => {
if (count === max) {
res.push(num);
} else if (count > max) {
max = count;
res = [num];
}
};
preOrder(root, node => {
if (node.val === num) {
count += 1;
} else {
update();
num = node.val;
count = 1;
}
});
update();
return res;
};
var preOrder = function(root, visit) {
root.left && preOrder(root.left, visit);
visit(root);
root.right && preOrder(root.right, visit);
};
Explain:
Pre-order traversal visiting can visit binary search tree's nodes value by ascending order.
Imaging you have an ordered array, find the most consecutive number(s).
Complexity:
- Time complexity : O(n).
- Space complexity : O(1).